Note: please do not cite the online version of this ms. It was published in 2004 in a special issue of the Italian Journal of Zoology along with papers by the participants of the workshop held in Rome in January 2002. The citation is Ital. J. Zool., 71:5-16.

Geometric Morphometrics: Ten Years of Progress Following the ‘Revolution’

Dean C. Adams¹, F. James Rohlf², and Dennis E. Slice³

¹ Department of Ecology, Evolution, and Organismal Biology, and
Department of Statistics
Iowa State University
Ames IA 50011-3223

² Department of Ecology and Evolution,
State University of New York at Stony Brook
Stony Brook, NY 11794-5245

³ Institute for Anthropology, University of Vienna and
Department of Medical Engineering
Wake Forest University School of Medicine
Winston-Salem, NC 27157-1022

Abstract

The analysis of shape is a fundamental part of much biological research. As the field of statistics developed, so have the sophistication of the analysis of these types of data. This lead to multivariate morphometrics in which suites of measurements were analyzed together using Canonical Variates analysis, Principal Components Analysis, and related methods. In the 1980s, a fundamental change began in the nature of the data gathered and analyzed. This change focused on the coordinates of landmarks and the geometric information about their relative positions. As a by-product of such an approach, results of multivariate analyses could be visualized as configurations of landmarks back in the original space of the organism rather than only as statistical scatterplots. This new approach, called "geometric morphometrics," had benefits that lead Rohlf and Marcus (1993) to proclaim a "revolution" in morphometrics. In this paper, we briefly update the discussion in that paper and summarize the advances in the ten years since the paper by Rohlf and Marcus. We also speculate on future directions in morphometric analysis.

Introduction

Comparing the anatomical features of organisms has been a central element of biology for centuries. The taxonomic classification of organisms, and understanding the diversity of biological life, were both historically based on descriptions of morphological forms. During the early twentieth century however, biology began the transition from a descriptive field to a quantitative science, and the analysis of morphology saw a similar ‘quantification revolution’ (Bookstein, 1998). Morphological studies included quantitative data for one or more measurable traits, which were summarized as mean values and compared among groups (e.g., Bumpus, 1898). The development of statistical methods such as the correlation coefficient (Pearson, 1895), analysis of variance (Fisher, 1935), and principal components analysis (Pearson, 1901; Hotelling, 1933) further advanced quantitative rigor. By the mid-twentieth century, quantitative description of morphological shape was combined with statistical analyses describing patterns of shape variation within and among groups, and the modern field of morphometrics began.

Morphometrics is the study of shape variation and its covariation with other variables (Bookstein, 1991; Dryden and Mardia, 1998). Traditionally, morphometrics was the application of multivariate statistical analyses to sets of quantitative variables such as length, width, and height (see below). In the late 1980’s and early 1990’s however, a shift occurred in the way morphological structures were quantified and how the data were analyzed. This shift emphasized methods that captured the geometry of the morphological structures of interest, and preserved this information throughout the analyses. In 1993 a review of the field of morphometrics called this new approach geometric morphometrics and suggested that this paradigm shift signaled a ”revolution in morphometrics” (Rohlf and Marcus, 1993). In the ten years since that review much progress has been made, and the field of geometric morphometrics has reached a more mature phase. Much of this is due to a greater understanding of the theoretical underpinnings of geometric morphometric methodology. The purpose of this paper is to briefly summarize the recent advances in the field of geometric morphometrics, describe a central protocol in modern morphometric analysis, and discuss several possible future directions being explored.

Traditional Morphometrics

In the 1960’s and 1970’s, biometricians began using the full arsenal of multivariate statistical tools to describe patterns of shape variation within and among groups. This approach, now called traditional morphometrics (Marcus, 1990; Reyment, 1991) or multivariate morphometrics (Blackith and Reyment, 1971), consisted of applying multivariate statistical analyses to sets of morphological variables. Usually, linear distance measurements were used, but sometimes counts, ratios, and angles were included. With these approaches, covariation in the morphological measurements was quantified, and patterns of variation within and among samples could be assessed. Statistical analyses typically included principal components analysis, factor analysis, canonical variates analysis (CVA), and discriminant function analysis. Many studies investigated allometry, or changes in shape with a change in size (Jolicoeur, 1963). Because linear distance measurements are usually highly correlated with size (Bookstein et al., 1985), much effort was spent developing methods for size correction, so that size-free shape variables could be extracted and patterns of shape variation elucidated (e.g., Sundberg, 1989; Jungers et al., 1995).

While multivariate morphometrics combined multivariate statistics and quantitative morphology, several difficulties remained. For instance, many methods of size correction were proposed, but there was little agreement on which method should be used. This issue is important because different size correction methods usually yield slightly different results. Second, the homology of linear distances was difficult to assess, because many distances (e.g., maximum width) were not defined by homologous points. Third, the same set of distance measures could be obtained from two different shapes because the location of where the distances were made relative to one another was not included in the data. For instance, if maximum length and maximum width were measured on both an oval and a teardrop, both objects could have the same height and width values, yet they are clearly different in shape Therefore, one expects the statistical power for distinguishing shapes to be much lower than it should be. Finally, it was not usually possible to generate graphical representations of shape from the linear distances because the geometric relationships among the variables were not preserved (a set of linear distances is usually insufficient to capture the geometry of the original object). Thus, some aspects of shape were lost.

The Geometric Morphometric Revolution

Because of these difficulties, researchers explored alternative methods of quantifying and analyzing morphological shape. Data that captured the geometry of the morphological structure was of particular interest, and methods to analyze such data were developed. This included methods for both outline and landmark data. Concurrent with these advances, David Kendall and other statisticians developed a rigorous statistical theory for shape analysis that made possible the combined use of multivariate statistical methods and methods for the direct visualization in biological form. Bookstein (1996a) referred to this as the “morphometric synthesis”. Below we review these developments, and survey the methods that lead to the “morphometric revolution” proclaimed by Rohlf and Marcus (1993).

Outline Methods

Outline methods were the first geometric morphometric methods to be used. While the bounding edge of a structure or region can be considered homologous across specimens, points collected to sample such curves do not have such clear correspondences. The approach usually used is to digitize points along an outline, fit the points with a mathematical function (usually some form of Fourier analysis), and then compare curves by using the coefficients of the functions as shape variables in multivariate analyses. Points in this multivariate parameter space (e.g., Fourier coefficient space) can be transformed back to the physical space of the organism and visualized as outlines. The earliest methods fit lengths of equally-space radii from a central point – either a landmark or the centroid of the object. Because this approach was limited to simple outlines, other methods were proposed such as using changes in the angle of tangents at each point along an outline, analyses of Dx and Dy values as a function of distance along the curve, or treating the coordinates of points along an outline as a sequence of complex numbers (see, for example, Rohlf 1990). While all of these methods “worked”, the problem was that statistical analyses based on the different methods gave different statistical results and there was no agreed upon theory that would enable a researcher to select the best approach (Rohlf, 1986).

Landmark Methods

Landmark-based geometric morphometric methods begin with the collection of two- or three-dimensional coordinates of biologically definable landmarks. Direct analysis of these coordinates as variables would be inappropriate as the effects of variation in position, orientation, and scale of the specimens are still present. Therefore, the non-shape variation must be mathematically removed prior to the analysis of such variables. Once non-shape variation has been eliminated, the variables become shape variables and may be used to statistically compare samples, and graphical representations of shape may be generated for comparison.

Superimposition methods eliminate non-shape variation in configurations of landmarks by overlaying them according to some optimization criterion. Several methods have been proposed, each using slightly different protocols and optimization criteria. Two-point registration (Bookstein’s shape coordinates) is a particularly simple superimposition method that laid the foundation for much of Bookstein’s development of shape theory in the late 1980’s. Generalized Procrustes analysis (GPA: called generalized least squares, GLS, in the earlier literature) superimposes landmark configurations using least-squares estimates for translation and rotation parameters. First, the centroid of each configuration is translated to the origin, and configurations are scaled to a common, unit size (by dividing by centroid size: Bookstein, 1986). Finally, the configurations are optimally rotated to minimize the squared differences between corresponding landmarks (Gower, 1975; Rohlf and Slice, 1990). The process is iterated to compute the mean shape, which is inestimable prior to superimposition. When much of the shape variation is limited to just a few landmarks, generalized resistant-fit (GRF) may be used to visualize this pattern of variation (Rohlf and Slice, 1990; Slice, 1996). GRF estimates superimposition parameters as medians, rather than least-squares estimates. Rotation angle and scale are found as medians of medians across subsets of landmarks, and translation is a simple coordinate-wise median. As in GPA, this procedure is iterated to allow a sample of specimens to be superimposed. In contrast to the use of GPA, the use of GRF does not lead to further statistical analyses.

After superimposition, shape differences can be described by the differences in coordinates of corresponding landmarks between objects. These differences have also been used as data in multivariate comparisons of shape variation (but see Bookstein, 1996b). Alternatively, the thin-plate spline can be used to map the deformation in shape from one object to another (Bookstein, 1991). Differences in shape represented in this fashion are a mathematically rigorous realization of D’Arcy Thompson’s (1917) idea of transformation grids, where one object is deformed or “warped” into another. Differences in shape among objects can then be described in terms of differences in the deformation grids depicting the objects. The parameters describing these deformations (partial warp scores) can be used as shape variables for statistical comparisons of variation in shape within and between populations. A related approach that received considerable attention in the early 1990’s was relative warp analysis, which is a principal components analysis of the partial warps -- shape variables, optionally weighted by spatial scale.

In addition to the superimposition approaches discussed here, several alternative procedures for obtaining shape information from landmark data have been proposed. These include: Euclidean distance matrix analysis (EDMA), finite element scaling analysis (FESA), and methods based on interior angles. These approaches are discussed in the Other Landmark Approaches section below.

The Maturing of Geometric Morphometrics

The revolution in morphometrics is leading to a shift in the way morphological studies are performed as analyses of linear distances give way to analyses based on landmarks and outlines. By the early 1990’s, the advantages of geometric morphometric methods were widely known, and biologists used landmark and outline methods with regularity to address a wide range of hypotheses. Additionally, biologists gained a better appreciation of the mathematical underpinnings of the landmark methods developed by Kendall and others in the 1980’s. The morphometric advances in the 1990’s were based on our improved understanding of the methods rather than fundamental theoretical breakthroughs.

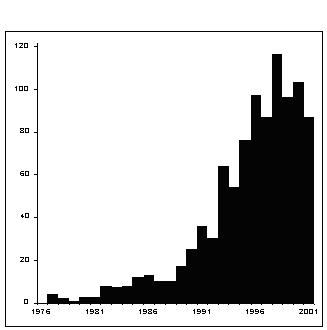
The increasing importance of geometric morphometric methods in the 1990s is evident in Figure 1 that shows the number of geometric morphometric publications per year from 1976 through 2001. The number of publications involving geometric morphometrics has increased dramatically during the 1990’s, though there appears to be a slight downturn in recent years. Our search was based on citations for only a small number of papers, so this downturn may not be entirely accurate. As the methodology becomes more widely known and accepted, authors have more citation options, and may feel less compelled to cite these “classic” papers in the field. It is certainly our experience (based on requests for advice and manuscript reviews) that more researchers than ever are using these methods, and we are confident that the geometric morphometric methods will have an increasing role in biological research.

Figure 1. Geometric morphometric citations per year from 1976 to 2001. Data from merging Lynch’s morphometric bibliographic data base (http://www.public.asu.edu/~jmlynch/geomorph/index.html) with Web of Science (http://www.isinet.com) citation searches for Rohlf and Slice, 1990; Bookstein, 1991; Rohlf and Marcus, 1993; and Marcus et al., 1996.

Along with increased application, significant theoretical advances have been made in recent years. For instance, in the early 1990’s many “competing” landmark methods existed, and criteria for choosing among them were lacking. A standard set of procedures for analyzing shape from landmark data has emerged and is now used in nearly all landmark-based morphometric studies (see Analysis of Landmark Data section below). These methods are based on Procrustes distances (or their tangent space approximations). Several recent studies have used both analytical and simulation approaches to compare landmark methods, demonstrating that these methods are the preferred methods for comparing shapes statistically (see Other Landmark Approaches section below). In addition, new approaches have also been proposed for the analysis of outline data. The method of sliding semilandmarks allows outlines to be combined with landmark data in one analysis, providing a richer description of shape (see Analysis of Outline Data section below). Finally, as geometric morphometric data are used to address more biological questions, new protocols are often needed. In the 1990’s we have seen the development of new methods that allow new kinds of applications (see Other Extensions of Geometric Morphometrics section below). The breadth of these “specialty” applications is a testament to the acceptance of geometric morphometric methods as a standard tool for addressing biological questions.

Analysis of Landmark Data

Today, nearly all landmark-based morphometric studies analyze shape with procedures based on Kendall’s shape space, Procrustes distance, or their tangent space approximations. This is based on the growing body of evidence from analytical and simulation studies showing that methods using Kendall’s shape space have the best statistical power, the lowest mean-squared error, and impose minimal constraints on the patterns of variation that can be detected (see Kent, 1994; Rohlf, 1999; 2000a; 2000b). Further, these methods are firmly grounded in a statistical theory for how shape is defined (Kendall, 1977) and how patterns of shape variation may be analyzed (Kendall, 1984; 1985; Small, 1996).

Using this approach, the analysis of landmark data can be summarized as a generalized Procrustes analysis (GPA), followed by projection of the aligned coordinates on a linear tangent space for multivariate analyses, and the graphical visualization of results in terms of the configurations of landmarks (Figure 2). GPA is an important procedure because it removes variation in digitizing location, orientation, and scale, and superimposes the objects in a common (though arbitrary) coordinate system. Additionally, the aligned specimens from GPA provide points that can be projected into a space that is tangent to Kendall’s shape space (Kendall, 1984; Rohlf, 1999; Slice, 2001). In this linear tangent space, distances between pairs of points (specimens) approximate the Procrustes distances between the corresponding pairs of landmark configurations. Partial warps from the thin-plate spline (which describe shape changes that can be described by local deformations, Bookstein, 1991) plus the uniform shape components (which describe shape changes that can be described by an infinite scale stretching or compression, Bookstein, 1996c; Rohlf and Bookstein, 2003) are a convenient set of shape variables that can be interpreted as axes for this linear tangent space. Scores on these axes can then be treated as multivariate data representing shape, and can be used in conventional multivariate analyses (e.g., Caldecutt and Adams, 1998; Bookstein et al., 1999; Adams and Rohlf, 2000; Gharaibeh et al., 2000; Rüber and Adams, 2001; Klingenberg and Leamy, 2001). It should be noted that the thin-plate spline is not required to perform a geometric morphometric analysis; any orthogonal projection to tangent space is sufficient (see Rohlf, 1999).

The final step of a morphometric analysis is graphically visualizing the results of the statistical analyses. An important strength of geometric morphometric methods is that graphical representations of results are possible in terms of the configurations of landmark points rather than as customary statistical scatterplots. This is possible because the geometry of shape is preserved throughout the analysis. Typically, shape differences are presented in a manner analogous to D’Arcy Thompson’s (1917) transformation grids, where one object, usually a mean shape, is deformed or “warped” into another using the thin-plate spline. Differences in shape among objects can then be described in terms of differences in the deformation grids depicting the objects.

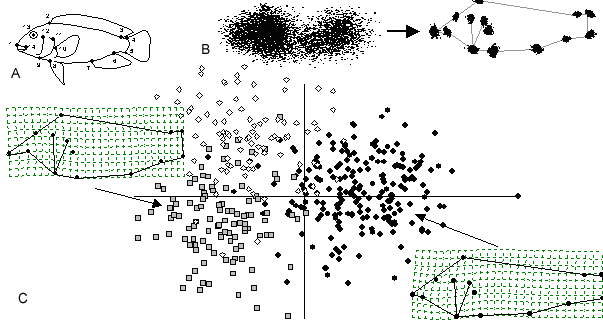
Figure 2. Graphical representation of the four-step morphometric protocol. A: Quantify raw data (landmarks recorded on body of cichlid fish), B: Remove non-shape variation (landmarks of 412 specimens before and after GPA), C: statistical analysis (CVA) and graphical presentation of results. Deformation grids for mean specimen for (right) Eretmodus cyanostictus and (left) Spathodus erythrodon (magnified by 3X to emphasize shape differences). Data from Rüber and Adams, 2001.

Other Landmark Approaches

Several alternative methods have been proposed that are based on matrices of distances between all pairs of landmarks or of interior angles from a triangulation of the landmarks. These methods have the intuitive appeal that because distances and angles are invariant to differences in the location and orientation of a configuration of landmarks a superimposition step is not required. They are also invariant to differences due to reflection, which can be convenient because it lets an investigator freely mix specimens from which landmarks have been recorded from either their left or right sides of bilaterally symmetric structures, but it also can be a limitation because it prevents certain shapes from being distinguished. Distances are, of course, not invariant to differences in size so some method of size scaling must be done in order to use them to study differences in shape. Rao and Suryawanshi (1996) proposed comparing samples of shapes using size-corrected logs of the distances between all pairs of landmarks. Rao and Suryawanshi (1998) proposed comparing shapes using angles from a triangulation of landmarks. Since the three interior angles of a triangle sum to a constant (p radians), only two arbitrarily selected angles from each triangle are used as shape variables. For more than 3 landmarks, there are many ways in which one can select the angles to be used. Lele and Richtsmeier (1991) proposed Euclidean distance matrix analysis, EDMA, to compare pairs of shapes. They first compute a matrix containing average distances between pairs of landmarks (Lele 1993 suggested using the method of moments for estimation) for each sample being compared. They are form matrices because they include both size and shape information. To compare two populations they compute a form difference matrix as the element-wise ratios of the interlandmark distances in the two matrices being compared. The amount of shape difference is given by T, the ratio of the largest to the smallest of the elements of the form difference matrix. Lele and Cole (1995, 1996) proposed another method that they claimed had higher statistical power in at least some cases.

How can one decide on which method to use? There are several basic statistical properties that can be used as a basis for evaluating methods. These include whether a method of estimation is consistent (i.e., does it gives the correct estimate as sample sizes become infinite), the magnitude of any systematic bias in estimating the mean shape (i.e., are the results correct for finite sample sizes), how close these estimates are to the true mean shape, and statistical power in detecting differences between mean shapes. They can most easily be investigated for the case of three landmarks in the plane. Lele (1993) reported that the method of estimating the mean shape in EDMA is consistent) under the simple model of independent isotropic variation at each landmark but Kent (1994) showed that Procrustes estimates of the average shape were also consistent under this same model. Rohlf (in prep.) used sampling experiments to reveal that methods based on interlandmark distances or angles were biased and had larger errors in their estimates of the mean shape unless the interlandmark distances were close to being equal. Rohlf (2000a) found that in many cases the statistical power for the methods based on interlandmark distances and angles were much lower (and never higher) than that for tests based on Procrustes methods. Lele and Cole (1996) reported rather different results but Rohlf (2000a) found a programming error in their simulations. Another important consideration in exploratory studies is that the methods themselves should not impose constraints on the patterns of variation one sees in the results of ordination analyses. Rohlf (1999; 2000b) found that the methods based on interlandmark distances and angles gave distinct patterns of covariation within and between samples that depended on their mean shapes. Figure 3 shows an example of the problem. This would mislead an investigator about covariation both within and between populations if such methods were used. No such problems were found when performing ordination analyses in the Kendall tangent space. For these reasons, we advocate using GPA as the basis for statistical analyses of shape variation.

Figure 3. Results from a sampling experiment comparing PCA ordinations based on Procrustes alignments and those based on interlandmark distances. A and B show isotropic scatter around five landmarks for 100 specimens. C The results of a principal components analysis using projections of Procrustes aligned specimens in the tangent space (equivalent to using partial warp scores and the uniform component). As expected, two distinct circular scatters are shown because the two populations differ only in mean shape. D The results of a principal components analysis using Rao & Suryawanshi (1996) shape variables. Note the different pattern of strong covariances within each group. The effect is more extreme than shown in Figure 9 in Rohlf (2000b) because the amount of variation at each landmark is smaller here to show that the distortion is not caused by landmarks “swapping places” as suggested by Lele and Richtsmeier (2001).

Analysis of Outline Data

An important limitation of landmark-based geometric morphometrics methods is that a sufficient number of landmarks may not be available to capture the shape of a structure. That is, there may be large regions of a structure where no biologically meaningful points can be identified. Important shape differences may also be located in the regions between landmarks. As described above, outlines of structures can be captured and analyzed using shape variables such as generated by an elliptic Fourier analysis, but this goes to the other extreme by ignoring differences in the relative positions of landmark points. An appealing solution is the sliding semilandmark method proposed by Bookstein (1997). This procedure extends the standard Procrustes superimposition procedure. In addition to optimally translating, scaling, and rotating the landmarks, the semilandmark points are slid along the outline curve until they match as well as possible the positions of the corresponding points along an outline in a reference specimen. The semilandmarks are constrained to retain their relative position on the outline curve. Once the optimally adjusted positions of the landmarks and semilandmarks are determined, they can all be treated in the same way in subsequent statistical analyses. Just as the thin-plate spline was conceived, developed, and presented by Bookstein long before it could be usefully applied to specific projects by independent researchers, the extension of morphometric software to include sliding landmarks has not yet been widely implemented and used.

Early applications of the sliding semilandmarks method by Bookstein and coworkers have been very useful in identifying interpretable morphological differences between control groups and groups of patients diagnosed with schizophrenia (Bookstein, 1997). In these applications, both landmarks and outlines have been combined, providing a richer description of overall shape. Bookstein et al. (1999) also used the method to investigate variation in the inner and outer frontal cranial profiles of hominids to reveal a striking and unexpected statistical identity of the inner profiles in modern Homo sapiens, several archaic Homo spp., and chimpanzees (Figure 4).

Figure 4. Procrustes fits of inner and outer frontal profiles for a) modern humans and b) modern and archaic humans, Australopithecines and chimpanzees using Procrustes analysis of landmarks and semilandmarks (reproduced from Bookstein et al., 1999).

The Future of the Revolution

In some respects, we expect the future of the geometric morphometrics revolution to be “more of the same.” The new methods have continually matured over the past decade, and scientists are increasingly using these approaches to more powerfully and efficiently investigate shape in many areas of biological research. The profile of these techniques, however, is still relatively low in the mainstream scientific literature. The methods do require some expertise in basic, though somewhat unfamiliar to most biologists, mathematical tools such as linear algebra and multivariate statistics. Some initial instruction in the proper use and interpretation of results is very helpful. This instruction is somewhat difficult to obtain for many researchers and students, but the demand for these methods is clearly there. Intensive workshops are now offered around the world, drawing a diverse and enthusiastic group of students, each more prepared and sophisticated than the last.

The following are a few areas we feel have yet to be fully explored, and that we anticipate will provide material for the future of geometric morphometrics.

Use of Three-Dimensional Data

One deficiency in modern morphometrics is that nearly all analyses are of two-dimensional representations of three-dimensional objects. This is not an inherent limitation of the morphometric methods. The extension of the algorithms for Procrustes superimpositions to specimens in three-dimensions is direct, and similar extensions have been developed for baseline registrations (e.g., Dryden and Mardia, 1998) and resistant fitting (Slice, 1996). Only a slight modification is necessary to produce interpolation functions for three-dimensional thin-plate splines (e.g., Figure 5). One important practical problem for 3D analyses is data acquisition. Three-dimensional digitizers, though more affordable and available than ever, still are expensive and/or limited in their resolution or usability for different sizes and configurations of specimens. A second, more fundamental, limitation is that of publication. Scientific papers are still largely limited to static, two-dimensional pieces of paper or computer screens that make the representation of volumetric changes challenging to say the least. As shown in Figure 5, one can appreciate, but not fully comprehend the volumetric differences being represented. As more journals go online one can anticipate the possibility of interactive publication graphics that would partially address this problem.

Figure 5. Example of three-dimensional thin-plate spline deformation grid (Gunz, 2001).

Combining Landmarks and Surfaces using Sliding SemiLandmarks

The logical extension of sliding landmark methods for curves (see above) is to extend the method to surfaces. This poses special challenges, as the equally spaced sampling of surfaces is a surprisingly complex problem. Researchers in Vienna working with Bookstein appear to have come up with a viable extension of the sliding landmark method to three-dimensional surfaces (Figure 6). The method involves densely sampling the surface with three-dimensional points using a standard digitizer and digitizing software, and triangulating the points into a surface mesh (CT, MRI, or other modality capable of producing surface meshes could also be used). On a representative specimen, a lower-resolution mesh is either measured manually or a high-resolution mesh is statistically “thinned” to reduce the number of vertices while maintaining a maximum amount of surface information. Once a reasonable number of vertices have been identified, data from multiple specimens are then splined onto the reference, and nearest surface points in individual specimens are then taken as homologous to those of the reduced mesh. These points are then allowed to slide in a plane tangential to the local curvature of the surface retaining their difference in the direction normal to it. As with outlines, the adjustments are repeated until the process converges. The entire data set can then be treated as multivariate data and subjected to more-or-less standard statistical analysis whose results can then be visualized as seen in Figure 6. In the case of sliding landmarks on two-dimensional curves, three-dimensional curves, and three-dimensional surfaces, all of the mathematical underpinnings have been set forth. All that is needed for this method to be generally employed is the independent evaluation of these methods and their packaging in easy-to-use software.

Figure 6. Sliding semilandmarks quantifying the surface of a skull (Mitteröcker, 2001; Mitteröcker and Gunz, 2002).

Allowing for Missing Data and Absent Structures

Another constraint on landmark-based geometric morphometrics of considerable importance is that all data used in a single analysis must be based on the same set of landmarks. This constraint has important implications. If specimens have missing landmarks (because they are broken or poorly preserved), either they must be eliminated from the analysis, or the missing landmarks must be eliminated from the dataset so that all specimens can be included in the analysis. Clearly, neither approach is generally desirable.

One approach to the problem of missing data is to use imputation methods to estimate the coordinates of missing landmarks and proceed with standard multivariate analysis. Simple methods for generating such estimates include mean-substitution, where mean coordinate values are used for the missing data, and regression methods, where estimates are based on regression equations predicting coordinates for variables with missing data from those with complete data. For the usual, normally distributed data, we know these methods tend to produce unbiased estimates of mean values, but tend to underestimate standard errors for those estimates and, thus, effect statistical testing (Little and Rubin, 1987). A method unique to geometric morphometrics is the estimation of missing data based on bending energy. That is, missing landmarks are positioned so as not to increase the bending energy in the shape difference between the specimen with missing data and a reference (Bookstein et al, 1999). Even for data without the strong geometric structure of landmark coordinates, the problem of missing data is extremely complex, but the availability of some reasonable ways to address the problem would be of considerable benefit to many morphometricians.

The requirement of complete and comparable sets of landmarks also means that there is no way to study the origination or elimination of structures within a data set. Comprehensive analyses of developmental series are therefore precluded, as are unrestricted phylogenetic comparisons of morphological change through evolutionary time. Simply avoiding the problem by focusing only on landmarks common to all specimens can affect the results of a study. Marcus et al (2000) conducted a three-dimensional landmark analysis of the orders of mammals to explore the possible limits of biological shape variation in a single study. They found that the maximum shape differences among taxa to be surprisingly low compared to what they expected intuitively (biologists tend to think of the orders of mammals as “extremely”’ different in shape). Their result was somewhat misleading because (as recognized by the original authors) in order to include some taxa (e.g., edentates), certain landmarks had to be ignored because they did not exist in those taxa (e.g., landmarks associated with dentition). Thus, the final set of common landmarks was greatly constrained in the range of variability it could reveal. New methods are needed that can allow for such complications.

Bookstein and Smith (2000) offered a possible solution based on the analysis of creases. Creases are local features (with direction and magnitude) of a thin-plate spline generated by extrapolating a properly oriented spline grid until a patch of the spline overruns itself – generating what is called a singularity (Bookstein, 2000; 2002). Creases were originally developed to provide a quantitative way to describe and evaluate thin-plate spline deformations, but they also have an interesting property that Bookstein and Smith suggest could be brought to bear on the problem of morphogenesis – they are invertible in the region of the singularity. That is, the process that generated the crease can be inverted and “reversed” to give the appearance of generating new tissues or structures.

Like the thin-plate splines, creases and their application to morphogenesis are mathematically sophisticated, and they have not yet found their way into any mainstream morphometric analysis. At this point we cannot predict the impact of this method on morphometric practice in the near future, but it does represent a first step toward addressing what is a fundamental problem in morphometrics – the complete modeling of development and evolution.

Estimating Landmark Covariance Structure

It is tempting to make conclusions about the patterns of variability at different landmarks and the covariation between landmarks after viewing a Procrustes superimposition of a sample of specimens onto their mean configuration. Inferences are more difficult than they might seem because, as noted by Rohlf and Slice (1990) and Slice (1993), it is possible for the superimposition itself to impose a pattern of covariation on the landmarks. Rohlf (in prep.) shows the results of a sampling experiment where the observed variation after Procrustes superimposition is very different from the model on which it was based. Walker (2000) documents some of the problems in estimating the pattern of variances and covariances of landmarks after a superimposition. These problems do not invalidate overall tests for shape differences. Dryden and Mardia (1998) show that if the original points have an isotropic scatter around each landmark, then the tangent coordinates will also be isotropic. While the proper estimation of the covariation at each landmark is an important problem that needs to be solved, it is not directly relevant for tests performed in Kendall’s tangent space. On the other hand, estimation of the relative variability at different landmarks and the patterns of covariance within and between landmarks should be of interest in many practical applications. Existing methods for estimating these variances and covariances are unsatisfactory because they can show unequal variances and strong covariances within and between landmarks when the actual variation is isotropic. Our best advice is still that of Rohlf and Slice (1990) who suggested performing simulations using the mean consensus configuration as a population mean to make sure that the patterns of variation are not just artifacts of the superimposition procedure. Additional work needs to be done in this area.

Morphometrics and Phylogenetics

One question that has received considerable attention, but has yet to be resolved, is what is the best way to use geometric morphometric data in phylogeny estimation. Because geometric morphometric data provide a rich description of morphological shape, it is natural to think that such data should be included when estimating phylogenetic trees. However, combining these two disciplines has been surprisingly difficult. One problem is that morphometric shape variables are continuous and capture the space of all possible shape variation whereas the cladistic procedures are based on discrete characters that can be interpreted separately. Another problem is that in cladistic procedures the Manhattan metric is used to define minimum length trees. This is a difficulty because shape variables such as partial warp scores are expressed relative to an arbitrary orientation for the reference configuration. Valid shape analyses ignore the effects of difference due to rotation but Manhattan distances between specimens are sensitive to such differences and they can lead to different minimum length trees being estimated (Rohlf, 1998; Adams and Rosenberg, 1998).

One approach has been to use a protocol where the original shape data (e.g., partial warp scores) are coded as discrete values based on some criterion and are then treated as input data for cladistic parsimony analyses (e.g., Fink and Zelditch, 1995; Swiderski et al., 2002; Zeldtich et al., 2000). Unfortunately, each partial warp score is coded separately, yet partial warp scores are not independent, and considered separately they are not descriptions of biologically meaningful characteristics. Using their procedure different arbitrary orientations of the reference configuration could lead to different minimum length trees. A further complication is that by discretely coding the partial warp scores information is lost (one consequence is that it is no longer possible to reconstruct the shape of a putative ancestor). See Adams and Rosenberg (1998) and Rohlf (1998) for further discussion. A recently proposed alternative is to quantify the shape of each anatomical structure separately (using partial warp scores), and inspect the shape variation of each structure for discontinuities (e.g., inspect a PCA plot for each structure separately). Discontinuities are then coded as discrete characters and treated as phylogenetic characters (see MacLeod, 2002). This approach avoids coding characters for each partial warp axis individually, but, of course, still loses shape information due to the coding procedure.

Recently, Bookstein (2002) proposed using the presence or absence of creases (see above) as a method of generating discrete characters from geometric morphometric data. For a fixed reference, Bookstein (2002) suggests that the presence or absence of these singularities in splines for different species may be used as homologous morphometric features, suitable for cladistic analysis. While creases potentially provide a procedure for generating phylogenetic characters from morphometric data, several questions remain. How can one determine that a particular crease in taxon A is homologous to the presence of a crease at a similar but not identical location in taxon B? Clearly more work is needed to fully explore this new approach.

An alternative approach is to use phylogenetic methods that can utilize geometric morphometric data in its original form rather than forcing them into integer codes in order to be compatible with the available software. Continuous maximum-likelihood (Felsenstein, 1988; 2002), squared-change parsimony, and neighbor joining methods may be used, as they can accommodate continuous data and do not depend upon arbitrary rotations of the multivariate data space (Rohlf, 2002). For phylogenetic inference, it may be useful to quantify the shape of many structures separately, and then combine the resulting shape variables in a single matrix for phylogenetic comparison. This approach allows the shapes of different regions of the organism to be used, while still preserving the continuous (and multivariate) nature of the shape variables. For continuous maximum-likelihood methods, an unresolved issue is how the phenotypic covariance matrix and the phylogeny can be estimated simultaneously (see Felsenstein, 2002). This is necessary because it is unrealistic to assume that shape variables evolve independently or that they are free from the direct effects of selection. In spite of this, we feel that using methods that can incorporate continuous, multivariate characters show the most promise for enabling the use of geometric morphometric data in phylogenetic systematic studies.

Other Extensions of Geometric Morphometrics

Numerous extensions to the basic methods of landmark-based geometric morphometrics have been proposed that could find their way into mainstream research or generate new directions of inquiry. Adams (1999) examined different ways to compare shapes of structures made up of articulated components – including fixing the angle of articulation, factoring out the effects of articulation, and combining independently computed shape variables (partial warp scores) for the components. Recently, Bookstein and his colleagues have developed general methods (using singular warps) for quantifying covariation between subsets of landmarks on the same structure using extensions of the two-block partial least-squares method (Bookstein et al. 2003). They use the method to characterize morphological integration of the vault, face, and cranial base in the genus Homo. Slice (1999) proposed a method by which the geometric morphometric analysis of static structures could be extended to parameterize repeating motions as trajectories through shape space, and in a similar spirit, O’Higgins et al. (2002) used principal components analysis to extract major features of facial expressions. Most recently, Slice (2002) presented a generalization of geometric motion analysis to include the analysis of non-repeating motions, and by extension, serially homologous structures.

Other researchers have demonstrated the use of geometric morphometrics together with sophisticated methods from other fields. The study of asymmetry, for instance, has attracted a great deal of attention and controversy over the past few years (Palmer and Strobeck, 1986; Palmer, 1996). Briefly, random departures from perfect symmetry in anatomical structures, fluctuating asymmetry (FA), are taken to reflect the stability of developmental processes. As with almost all questions in morphometrics, most work has concentrated on the analysis of traditional measures like angles and ratios. Klingenberg and McIntyre (1998), however, presented an analysis of FA using shape variables derived from geometric morphometrics to study levels of integration, thus benefiting from all the advantages of comprehensiveness, power, and visualization potential of these methods. Regardless of the ultimate utility of FA as a measure for developmental stability, Mardia, et al. (2000), and Kent and Mardia (2001) provide the theoretical basis of the use of geometric morphometrics in future applications like these. Another area where modern morphometric methods may make a significant contribution is quantitative genetics. Klingenberg et al. (2001) use Procrustes-derived shape variables to map quantitative trait loci influencing the shape of the mouse mandible, and Klingenberg and Leamy (2001) use the same kinds of data to explore the relationship between genetic and phenotypic covariance and use Lande’s (1979) multivariate version of the breeder’s equation to estimate and evaluate potential responses to selection. Monteiro et al. (2002) suggest the use of Goodall’s (1991) F-statistic, the multivariate regression of offspring onto parental shape, and analysis of relative warp scores to estimate the heritability of shape. They find these methods more powerful than the analysis of an exhaustive list of interlandmark distances and also benefit from the visualization capabilities of geometric morphometrics.

Conclusion

In the ten years following the morphometric “revolution,” much progress has been made and the field of geometric morphometrics has greatly matured. A decade ago, the morphometric toolbox contained many techniques for landmark and outline data, and few logical criteria existed for choosing one method over another. Today the toolbox is much less cluttered, and a standard protocol based on Procrustes methods, with various “extensions” for particular data types, is sufficient for most applications. For landmark data, a standard protocol based on Procrustes methods is now widely accepted and used in nearly all landmark-based morphometric studies. Additionally, by using sliding semilandmarks, outline data may also be analyzed using Procrustes methods. This is a significant improvement for outline analysis, as the statistical properties for Procrustes approaches are well understood, and this allows both landmarks and outlines to be combined in one analysis.

The development of special extensions to Procrustes methods have allowed applications to address particular biological hypotheses. These procedures have greatly increased the use of geometric morphometric methods, and helped bring them into the mainstream of biological research. The use of geometric morphometric data as input into other sophisticated analyses clearly deserves further attention, and has the potential to significantly impact research in these other fields. We anticipate that over the next few years the geometric morphometric methods that were developed to address shortcomings of what was then the traditional approach to shape analysis will themselves evolve into a standard research protocol - perhaps even becoming the new “traditional” morphometrics. We look forward to these exciting new developments.

Acknowledgements

This work was supported in part by grants (DEB-0122281) from the Population Biology program of the National Science Foundation to DCA and (DEB-0212023) from the Systematic Biology program of the National Science Foundation to FJR. Work by DES was supported, in part, by the Austrian Ministry of Education, Science, and Culture, and the Austrian Council for Science and Technology (grant number: AD 387/25-30 to Horst Seidler) and Dr. Edward G. Hill and members of the Winston-Salem community. The helpful comments of Waleed AlGharaibeh, Windsor Aguirre, Jesús Marugán, Paola Ortiz, and Alexandra Valentin were greatly appreciated. This chapter is contribution no. 1106 from the Graduate Studies in Ecology and Evolution, State University of New York at Stony Brook.

Literature Cited

Adams, D. C. 1999. Methods for shape analysis of landmark data from articulated structures. Evolutionary Ecology Research. 1:959-970.

Adams, D. C., and F. J. Rohlf. 2000. Ecological character displacement in Plethodon: biomechanical differences found from a geometric morphometric study. Proceedings of the National Academy of Sciences, U.S.A. 97:4106-4111.

Adams, D. C., and M. S. Rosenberg. 1998. Partial warps, phylogeny, and ontogeny: a comment on Fink and Zelditch (1995). Systematic Biology. 47:168-173.

Blackith, R., and R. A. Reyment. 1971. Multivariate morphometrics. Academic Press, New York.

Bookstein, F. L. 1986. Size and shape spaces for landmark data in two dimensions. Statistical Science. 1:181-222.

Bookstein, F. L. 1991. Morphometric tools for landmark data: geometry and biology. Cambridge University Press, Cambridge.

Bookstein, F. L. 1996a. Biometrics, biomathematics and the morphometric synthesis. Bulletin of Mathematical Biology. 58:313-365.

Bookstein, F. L. 1996b. Combining the tools of geometric morphometrics. In Advances in morphometrics. (Marcus, L.F., M. Corti, A. Loy, G. Naylor, and D. Slice, eds.). Pp. 131-151. Plenum Press, New York.

Bookstein, F. L. 1996c. A standard formula for the uniform shape component in landmark data. In Advances in morphometrics. (Marcus, L.F., M. Corti, A. Loy, G. Naylor, and D. Slice, eds.). Pp. 153-168. Plenum Press, New York.

Bookstein, F. L. 1997. Landmark methods for forms without landmarks: Localizing group differences in outline shape. Medical Image Analysis. 1:225-243.

Bookstein, F. L. 1998. A hundred years of morphometrics. Acta Zoologica Academiae Scientiarum Hungaricae. 44:7-59.

Bookstein, F.L. 2000. Creases as local features of deformation grids. Medical Image Analysis. 4:93-110.

Bookstein, F. L. 2002. Creases as morphometric characters. In Morphology, shape and phylogeny. (MacLeod, N., and P. L. Forey, eds.). Pp. 139-174. Systematics Association Special Volume Series 64. Taylor and Francis, London.

Bookstein, F. L., B. Chernoff, R. L. Elder, , J. M. Humphries, Jr., G. R. Smith, , and R. E. Strauss. 1985. Morphometrics in evolutionary biology. Special publication 15. Academy of Natural Sciences Press, Philadelphia.

Bookstein, F. L., P. Gunz, P. Mitteröcker, H. Prossinger, K. Schäfer, and H. Seidler. 2003. Cranial integration in Homo: Singular warps analysis of the midsagittal plane in ontogeny and evolution. Journal of Human Evolution. (In Press).

Bookstein, F. L., K. Schäfer, H. Prossinger, H. Seidler, M. Fieder, C. Stringer, G. W. Weber, J.-L. Arsuaga, D. E. Slice, F. J. Rohlf, W. Recheis, A. J. Mariam, and L. F. Marcus. 1999. Comparing frontal cranial profiles in archaic and modern Homo by morphometric analysis. Anatomical Record (New Anatomist). 257:217-224.

Bookstein, F. L. and B. R. Smith. 2000. Inverting development: geometric singularity theory in embryology. In Mathematical Modeling, Estimation, and Imaging. (Wilson, D., H. Tagare, F. Bookstein, F. Préteauz, and E. Dougherty, eds). Pp. 139-174. Proc. SPIE, vol. 4121.

Bumpus, H. C. 1898. The elimination of the unfit as illustrated by the introduced sparrow Passer domesticus. Biological Lectures, Marine Biological Laboratory, Woods Hole. 11:209-226.

Caldecutt, W. C., and D. C. Adams. 1998. Morphometrics of trophic osteology in the threespine stickleback, Gasterosteus aculeatus. Copeia 1998:827-838.

Dryden, I. L., and K. V. Mardia. 1998. Statistical shape analysis. John Wiley & Sons, New York.

Felsenstein, J. 1988. Phylogenies and quantitative characters. Annual Review of Ecology and Systematics. 192:445-471.

Felsenstein, J. 2002. Quantitative characters, phylogenies, and morphometrics. In Morphology, shape and phylogeny. (MacLeod, N., and P. L. Forey, eds.). Pp. 27-44. Systematics Association Special Volume Series 64. Taylor and Francis, London.

Fink, W. L., and M. L. Zelditch. 1995. Phylogenetic analysis of ontogenetic shape transformations: a reassessment of the piranha genus Pygocentrus (Teleostei). Systematic Biology. 44:343-360.

Fisher, R. A. 1935. The logic of inductive inference. Journal of the Royal Statistical Society. 98:39-82.

Gharaibeh, W. S., F. J. Rohlf, D. E. Slice, and L. E. DeLisi. 2000 A geometric morphometric assessment of change in midline brain structural shape following a first Episode of schizophrenia. Biological Psychiatry. 48:398-405.

Goodall, C. R. 1991. Procrustes methods in the statistical analysis of shape. Journal of the Royal Statistical Society, Series B. 53:285-339.

Gower, J. C. 1975. Generalized Procrustes analysis. Psychometrika. 40:33–51.

Gunz, P. 2001. Using semilandmarks in three dimensions to model human neurocranial shape. Masters Thesis. University of Vienna, Austria.

Hotelling, H. 1933. Analysis of a complex of statistical variables into principal components. Journal of Educational Psychology. 24:417-441, 498-520.

Jolicoeur, P., 1963. The generalization of the allometry equation. Biometrics. 19:497-499.

Jungers, W. L., A. B. Falsetti, and C. E. Wall. 1995. Shape, relative size, and size-adjustments in morphometrics. Yearbook of Physical Anthropology 38:137-161.

Kendall, D. G. 1977. The diffusion of shape. Advances in Applied Probability. 9:428-430.

Kendall, D. G. 1984. Shape-manifolds, Procrustean metrics and complex projective spaces. Bulletin of the London Mathematical Society 16:81-121.

Kendall, D. G. 1985. Exact distributions for shapes of random triangles in convex sets. Advances of Applied Probability 17:308-329.

Kent, J. T. 1994. The complex Bingham distribution and shape analysis. Journal of the Royal Statistical Society, Series B. 56:285-299.

Kent, J. T. and K. V. Mardia. 2001. Shape, Procrustes tangent projections and bilateral symmetry. Biometrika. 88:469-485.

Klingenberg, C. P. and L. J. Leamy. 2001. Quantitative genetics of geometric shape in the mouse mandible. Evolution. 55:2342-2352.

Klingenberg, C. P. and G. S. McIntyre. 1998. Geometric morphometrics of developmental instability: analyzing patterns of fluctuating asymmetry with Procrustes methods. Evolution. 52: 1363-1375.

Klingenberg, C. P., L. J. Leamy, E. J. Routman, and J. M. Cheverud. 2001. Genetic architecture of mandible shape in mice: effects of quantitative trait loci analyzed by geometric morphometrics. Genetics. 157:785-802.

Lande, R. 1979. Quantitative genetic analysis of multivariate evolution, applied to brain:body size allometry. Evolution. 33:402-416.

Lele, S. 1993. Euclidean distance matrix analysis: estimation of mean form and form differences. Mathematical Geology. 25:573-602.

Lele, S., and T. M. Cole III. 1995. Euclidean distance matrix analysis: a statistical review. In Current Issues in Statistical Shape Analysis. Volume 3. Pp. 49-53. University of Leeds, Leeds.

Lele, S., and T. M. Cole III. 1996. A new test for shape differences when variance-covariance matrices are unequal. Journal of Human Evolution. 31:193-212.

Lele, S., and J. T. Richtsmeier. 1991. Euclidean distance matrix analysis: a coordinate free approach for comparing biological shapes using landmark data. American Journal of Physical Anthropology. 86:415-427.

Lele, S. and J. T. Richtsmeier. 2001. An invariant approach to statistical analysis of shapes. Chapman & Hall: New York. 308 pp.

Little R. J. A. and D. B. Rubin. 1987. Statistical Analysis with Missing Data. John Wiley & Sons, New York.

MacLeod, N. 2002. Phylogenetic signals in morphometric data. In Morphology, shape and phylogeny. (MacLeod, N., and P. L. Forey, eds.). Pp. 100-138. Systematics Association Special Volume Series 64. Taylor and Francis, London.

Marcus, L. F. 1990. Traditional morphometrics. In Proceedings of the Michigan morphometrics workshop. (Rohlf, F. J., and F. L. Bookstein, eds.). Pp. 77-122. Special Publication Number 2. University of Michigan Museum of Zoology, Ann Arbor.

Marcus L. F., M. Corti, A. Loy, G. J. P. Naylor, and D. E. Slice. 1996. Advances in Morphometrics. Plenum Press. New York.

Marcus, L. F., E. Hingst-Zaher, and H. Zaher. 2000. Application of landmark morphometrics to skulls representing the orders of living mammals. Hystrix. 11:27-47.

Mardia, K. V., F. L. Bookstein, and I. J. Moreton. 2000. Statistical assessment of bilateral symmetry of shapes. Biometrika. 87:285-300.

Mitteröcker P. 2001. Assessment of human preadolescent cranial growth and its implications for human evolution. Masters Thesis. University of Vienna, Austria.

Mitteröcker P. and P. Gunz. 2002. Semilandmarks on curves and surfaces in three dimensions. Am. J. Phys. Anthropol. Suppl. 34: 114-115.

Monteiro, L. R., J. A. F. Diniz-Filho, S. F. dos Reis, and E. D. Araújo. 2002. Geometric estimates of heritability in biological shape. Evolution. 56:563-572.

O'Higgins, P, N. Jones, A. Ghattaura, P. Hammond, T. Hutton, and M. Carr. 2002. Geometric morphometric approaches to the study of soft tissue growth and expression in the human face. American Journal of Physical Anthropology. 117 (S34):119.

Palmer, A. R. 1996. Waltzing with asymmetry. BioScience. 46:518-532.

Palmer, A. R. and C. Strobeck. 1986. Fluctuating asymmetry: measurement, analysis, patterns. Annual Review of Ecology and Systematics. 17:391-421.

Pearson, K. 1895. Note on regression and inheritance in the case of two parents. Proceedings of the Royal Society of London. 58:240-242.

Pearson, K. 1901. On lines and planes of closest fit to systems of points in space. Philosophical Magazine Series 6. 2:559-572.

Rao, C. R., and S. Suryawanshi. 1996. Statistical analysis of shape of objects based on landmark data. Proceedings of the National Academy of Sciences, U.S.A. 93:12132-12136.

Rao, C. R., and S. Suryawanshi. 1998. Statistical analysis of shape through triangulation of landmarks: a study of sexual dimorphism in hominids. Proceedings of the National Academy of Sciences, U.S.A. 95:4121-4125.

Reyment, R. A. 1991. Multidimensional paleobiology. Pergamon Press, New York.

Rohlf, F. J. 1986. Relationships among eigenshape analysis, Fourier analysis, and analysis of coordinates. Mathematical Geology. 18: 845-854.

Rohlf, F. J. 1990. Fitting curves to outlines. Proceedings of the Michigan morphometrics workshop. In Proceedings of the Michigan morphometrics workshop. (Rohlf, F. J., and F. L. Bookstein, eds.). Pp. 167-177. Special Publication Number 2. University of Michigan Museum of Zoology, Ann Arbor.Rohlf, F. J. 1998. On applications of geometric morphometrics to studies of ontogeny and phylogeny. Systematic Biology. 47:147-158.

Rohlf, F. J. 1999. Shape statistics: Procrustes superimpositions and tangent spaces. Journal of Classification. 16:197-223.

Rohlf, F. J. 2000a. Statistical power comparisons among alternative morphometric methods. American Journal of Physical Anthropology. 111:463-478.

Rohlf, F. J. 2000b. On the use of shape spaces to compare morphometric methods. Hystrix. 11:9-25

Rohlf, F. J. 2002. Geometric morphometrics and phylogeny. In Morphology, shape and phylogeny. (MacLeod, N., and P. L. Forey, eds.). Pp. 175-193. Systematics Association Special Volume Series 64. Taylor and Francis, London.

Rohlf, F. J. and F. L. Bookstein. 2003. Computing the uniform component of shape variation. Systematic Biology. 53:000-000.

Rohlf, F.J. and L. F. Marcus. 1993. A revolution in morphometrics. Trends in Ecology and Evolution 8:129-132.

Rohlf, F. J. and D. E. Slice. 1990. Extensions of the Procrustes method for the optimal superimposition of landmarks. Systematic Zoology 39:40-59.

Rüber, L. and D. C. Adams. 2001. Evolutionary convergence of body shape and trophic morphology in cichlids from Lake Tanganyika. Journal of Evolutionary Biology. 14:325-332.

Slice, D. E. 1993. Extensions, comparisons, and applications of superimposition methods for morphometric analysis. Ph.D. dissertation. Department of Ecology and Evolution. State University of New York, Stony Brook, New York.

Slice, D. E. 1996. Three-dimensional, generalized resistant fitting and the comparison of least-squares and resistant-fit residuals. In Advances in morphometrics. (Marcus, L.F., M. Corti, A. Loy, G. Naylor, and D. Slice, eds.). Pp. 179-199. Plenum Press, New York.

Slice, D. E. 1999. Geometric motion analysis. American Journal of Physical Anthropology. 253-254, Suppl. 28.

Slice, D. E. 2001. Landmark coordinates aligned by Procrustes analysis do not lie in Kendall’s shape space. Systematic Biology. 50:141-149.

Slice, D.E. 2002. The application and analysis of generalized shape trajectories. Collegium Antropologicum. 26(Supplement): 192.

Small, C. G. 1996. The statistical theory of shape. Springer-Verlag, New York.

Sundberg, P. 1989. Shape and size-constrained principal component analysis. Systematic Zoology. 38:166-168.

Swiderski, D. L., M. L. Zelditch, and W. L. Fink. 2002. Comparability, morphometrics and phylogenetic systematics. In Morphology, shape and phylogeny. (MacLeod, N., and P. L. Forey, eds.). Pp. 67-99. Systematics Association Special Volume Series 64. Taylor and Francis, London.

Thompson, D. W. 1917. On growth and form. Cambridge University Press, London.

Walker, J. A. 2000. The ability of geometric morphometric methods to estimate a known covariance matrix. Systematic Biology. 49:686-696.

Zelditch, M. L., D. L. Swiderski, and W. L. Fink. 2000. Discovery of phylogenetic characters in morphometric data. In Phylogenetic analysis of morphological data. (Weins, J. J. ed.). Pp. 37-83. Smithsonian Institution Press, Washington.

Last revision: February 13, 2009